El problema del cocodrilo y la cebra, planteado en un examen de matemáticas para estudiantes de Escocia que se presentaban a la Scottish Qualifications Authority (SQA), una prueba de acceso a la universidad, ha resultado tal reto para los propios estudiantes que muchos, incapaces de resolverlo, terminaron la prueba entre lágrimas -y no de cocodrilo, precisamente.
Tal fue la complejidad de la prueba presentada en mayo de este año que la nota mínima se tuvo que reducir en un 34%, en comparación con el 45% del año anterior. Frustración, indignación y lágrimas por parte de los estudiantes, de entre 16 y 18 años, que no tardaron en manifestar sus quejas en redes sociales y de unirse para firmar dos peticiones en línea para formalizar la queja y reclamarla.
El problema
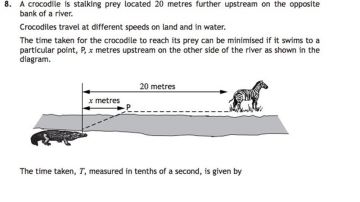
Un cocodrilo acecha a su presa, que está situada a 20 metros de distancia en la otra orilla del río. Los cocodrilos se desplazan a una velocidad diferente en tierra y en agua.
El tiempo que necesita el cocodrilo para llegar hasta su presa puede reducirse si nada 'x' metros corriente arriba hasta un punto 'P', situado en la otra orilla, tal y como se muestra en la imagen superior. El tiempo que tarda, 'T', se mide en décimas de segundo y está formado por la fórmula T (x) = 5 v36+x2+ 4 (20-x).
1. Calcula el tiempo que tardará el cocodrilo si no va por tierra.
2. Calcula el tiempo que tardará el cocodrilo si nada la distancia más corta posible.
3. Entre estos dos extremos, cuál es el valor de 'X' que minimiza el tiempo que tarda. Encuentra este valor para determinar cuál es el mínimo tiempo posible.
La solución
En el blog Calle Mayor han publicado el resultado al completo paso a paso. Hay que tener en cuenta que si se minimiza el tiempo en el agua (por los catetos) se recorren 20 metros a la máxima velocidad, pero también se recorre la máxima distancia posible. Por el contrario, en el agua se recorre la minima distancia a la menor velocidad.
Así, la parte izquierda de la fórmula sería el cálculo de la hipotenusa (velocidad en el agua) y la de la derecha la del desplazamiento por tierra. De este modo:
- La distancia a tierra es de 6m (36=6^2).
- La velocidad del cocodrilo en el agua es de 0,5 segundos por metro.
- La velocidad del cocodrilo en la tierra es de 0,4 segundos por metro.
- La proporción entre la velocidad tierra/agua es de 0,4s/0,5s = 0,8s (tierra) /1s (agua).
En una circunferencia goniométrica, de radio 1, habría que encontrar el ángulo que diera el coseno (la horizontal) con esta proporción de 0,8, según se expone en la solución del blog. Si fuera mayor que esta proporción, avanzaría demasiado rato más despacio (agua), y si fuera menor, recorrería demasiado camino. Se resuelve así: arco coseno de 0,8=36,86º, es decir, el ángulo en el que nadará el cocodrilo con respecto a la paralela.
En este momento, habría que calcular la 'X'. En esta circunferencia, el cateto mide 0,6 (Sen 36,86º=0,6). Como el cateto con el que se trabaja mide 6 metros, existe una relación la relación es 6/0,6, de modo que los valores son 10 veces con respecto a la circunferencia goniométrica. El radio (longitud nadada) será entonces 1x10 = 10 metros. Y la distancia equivalente terrestre (el otro cateto) será la proporción calculada antes (0,8) mutiplicada por este factor 10.
La 'X' son 8 metros
Más sencillo, pero con igual resultado, es este otro modo de resolver el problema:
